Hinreichendes
Kriterium für
Übereinstimmung
von Funktion und
ihrer Tayloreihe |
 |
Worum gehts |
|
Wir geben nun endlich ein hinreichendes Kriterium an, das uns sagt,
wann eine Funktion mit ihrer Taylorreihe übereinstimmt.
Das Kriterium ist unmittelbar verständlich, wenn man sich
Funktion und Taylorreihe bildlich vorstellt (Bild siehe unten).
|
 |
Satz |
|
Eine Funktion stimmt genau dann
mit ihrer
Taylorreihe überein (konvergiert gegen ihre Taylorreihe),
wenn das Restglied (für n gegen unendlich) gegen Null geht:
 |
|
 |
Bild zum Satz |
|
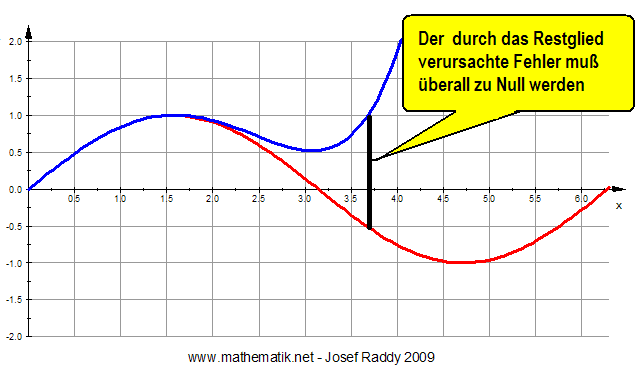
|
 |
Hinweis |
|
Wenn das Restglied gegen Null konvergiert, dann konvergiert die Reihe
gegen die Funktion
(nach den oben erwähnten Satz).
Da aber die Reihe nicht gleichzeitig divergieren kann, wenn sie gegen
eine beschränkte Funktion
konvergiert, ist der Konvergenzbereich der Reihe gleich dem der
Funktion, sodass
sich eine Berechnung des Konvergenzbereichs erübrigt.
Aus diesem Grund ist es ein hinreichendes Kriterium, wenn der
Rest R(x) gegen Null geht. |
| |
|