Praktische Anwendung
des hinreichenden
Kriteriums:
Beispiel: Sinusfunktion |
 |
Erklärung |
|
Wir haben das hinreichende Kriterium bereits kennengelernt, dass sagt,
wann eine Funktion mit ihrer Taylorreihe übereinstimmt: Das Restglied
muß für alle x und n→∞ zu Null werden. Wir
zeigen nun am Beispiel
der Sinusfunktion, wie man das Kriterium praktisch anwendet.
Die Formel für das Restglied haben wir im Kurs Taylorpolynome
kennengelernt:
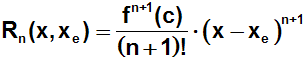
Nun fragen wir uns, wie man überprüfen kann, ob das Restglied
zu
einer gegebenen Funktion (z.B. Sinusfunktion) für alle x
zu Null wird,
wenn n gegen Unendlich geht. Also müssen wir auf der rechten Seite
den Grenzwert n→∞ bilden:
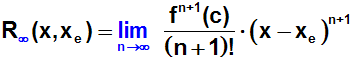
Wir schreiben das Restglied etwas anders:
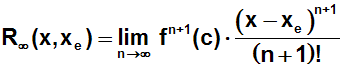
Der Term (x–xe)n+1/(n+1)!
hat für n→∞ den Grenzwert Null.
Dies kann man mit dem Quotientenkriterium beweisen,
was wir im Anhang dieses Kapitels nachholen:
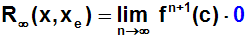
Nun fragen wir uns, ob f n+1(c) nur endliche Werte annehmen
kann,
oder ob dieser Term den Wert Unendlich annehmen kann.
Dazu bilden wir die Ableitungen f n:
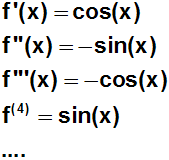
Wie man sieht wiederholen sich die Ableitungen ab der 4.Ableitung.
Alle diese Ableitungen [cos(x), sin(x), –cos(x), –sin(x)] haben an der
Stelle c
einen endlichen Wert, denn keine der Ableitungen nimmt an irgendeiner
Stelle einen unendlichen Wert an (und somit auch nicht an der Stelle c).
Somit ist f n+1(c) für alle n stets eine endliche Zahl k. Wir
können schreiben:
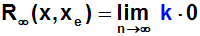
Der Grenzwert auf der rechten Seite ist gleich Null, denn wenn man eine
endliche Zahl mit einem Term multipliziert, der zu Null wird, erhält man
Null.
Ergebnis:
Weil der Rest Rn(x,xe) für
alle x gegen Null geht, ist die Sinusfunktion
mit ihrer Taylorreihe identisch.
|
| |
|