Beweis:
(x–xe)n+1/(n+1)!
=0
für n→∞ |
 |
Anhang: Beweis, dass
(x–xe)n+1/(n+1)!
=0 für n→∞ |
|
Wir wollen folgenden Grenzwert beweisen:
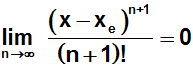
Der Grenzwert ist zum Beispiel gleich Null, wenn die zugehörige Reihe
konvergiert,
denn eine notwendige Bedingung für die Konvergenz einer Reihe ist,
dass die Folge der Summanden gegen Null geht (Nullfolgenkriterium):
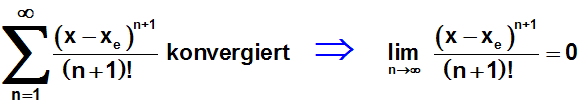
Die Konvergenz der Reihe kann wiederum mit dem Quotientenkriterium
leicht
bewiesen werden, was wir nun tun: Wir bilden den Grenzwert des
Quotienten
zweier aufeinanderfolgender Glieder für n gegen Unendlich:
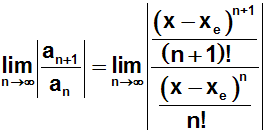
Den Doppelbruch mit den Mitteln der Bruchrechnung auflösen:
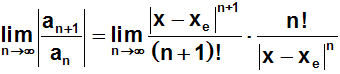
Kürzen:
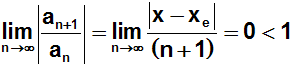
Weil der Quotient kleiner 1 ist, haben wir bewiesen, dass die Reihe
konvergiert,
und somit konvergiert auch die Folge der Summanden.
|
| |
|