Die Arten einer Umformung
|
 |
1.Äquivalenzumformungen |
|
Eine Äquivalenzumformung ist, wie wir wissen, eine Umformung, bei
der sich
die Lösungsmenge nicht ändert. Bestimmte Rechenoperationen (z.B. das
Potenzieren mit einer
ungeraden Zahl) bilden sowohl bei Gleichungen als
auch bei
Ungleichungen eine Äquivalenzumformung. Beispiel:
Die Lösungsmenge der folgenden Ungleichung besteht aus allen
Zahlen x,
die größer als 2 sind:
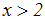
Jetzt potenzieren wir die Ungleichung mit 3. Die Lösungsmenge
bleibt gleich:
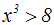
Im Kapitel 2 und 3 werden wir lernen, das folgende Rechenoperationen
Äquivalenzumformungen für Ungleichungen darstellen:
1. Addition oder Subtraktion einer beliebigen Zahl.
2. Multiplikation oder Divison mit einer positiven Zahl.
3. Multiplikation oder Divison mit einer negativen Zahl,
wenn man das Ungleichheitszeichen umdreht.
4. Termumformungen durch Rechengesetze.
5. Zerlegung von Produkten und Quotienten.
6. Anwenden einer streng-monoton steigenden Funktion,
(deren Definitionsbereich groß genug ist).
7. Anwenden einer streng-monoton fallenden Funktion,
(deren Definitionsbereich groß genug
ist),
wenn man gleichzeitig das Ungleichheitszeichen umdreht.
|
 |
2.Gewinnumformungen
(Folgeumformung, Implikation) |
|
Eine Gewinnumformung ist eine Umformung, bei der Lösungen
hinzukommen
können. Man nennt diese falschen Lösungen Scheinlösungen.
Bei Gleichungen hatten wir zwei Arten von Gewinnumformungen
unterschieden:
1. Erweiterung des Definitionsbereiches der Funktion
2. Anwenden einer nicht-bijektiven Funktion (z.B. Quadrieren)
Bei Ungleichungen gibt es nur eine Art von
Gewinnumformung:
1. Erweiterung des Definitionsbereiches
Bijektive Funktionen spielen bei Ungleichungen keine Rolle, sie können
sowohl
Äquivalenz-, Gewinn- oder Verlustumformungen sein (mehr im Kapitel 3): |
|
|
 |
3.Verlustumformungen |
|
Bei einer Verlustumformung gehen Lösungen verloren, und somit sind
sie verboten.
Bei Gleichungen können zwei Arten von Umformungen zu einer Verlustumformung
führen, d.h. es können Lösungen verloren gehen:
1. Einschränken des Definitionsbereiches der Funktion
2. Falsches Anwenden von Rechengesetzen
(Nichtbeachten des
Definitionsbereichs der Rechengesetze)
Bei Ungleichungen kann noch eine dritte Art von Umformungen zum
Verlust
von
Lösungen führen, also eine Verlustumformung darstellen:
3. Das Anwenden einer nicht streng monoton verlaufenden Funktion
|
|
|
 |
4.Umformung, die auf undefinierte
Ausdrücke führt |
|
Wie bei den Gleichungen kann auch bei Ungleichungen eine Umformung
zu
einem undefinierten Ausdruck führen. Beispiel:
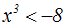
Wir ziehen die 3. Wurzel:
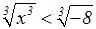
Wir werden später zeigen, wie man dieses Problem umgeht, und die
Gleichung
doch noch lösen kann. |
|
|
|