Lösungsmengen
die aus mehreren
Intervallen bestehen |
 |
Lösungsmenge besteht aus
mehreren Intervallen |
|
Die Lösungsmenge einer Ungleichung kann auch aus mehreren
Intervallen bestehen.
So besteht zum Beispiel die Lösungsmenge der Ungleichung
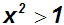
aus allen Zahlen, die entweder kleiner als 1 sind oder die größer als 1
sind:
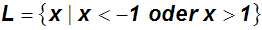
Gesprochen als:
Die Lösungsmenge L besteht aus allen Elementen x für die gilt: x kleiner
1 oder x größer als 1.
In dieser Formel ersetzt man das Wort "oder" oft durch das ODER-Zeichen,
dass wir aus dem Kurs
Aussagenlogik kennen:
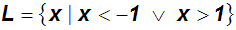
In der Klammerschreibweise (Intervallschreibweise) müssen wir die
Vereinigungsmenge
der beiden Intervalle bilden:
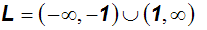
|
 |
Lösungsmenge besteht aus
einem Intervallen |
|
Besteht die Lösungsmenge einer
Ungleichung nur aus einem Intervall,
dann kann man die Lösungsmenge in der Mengenschreibweise oder
in der Klammerschreibweise (Intervallschreibweise) angeben.
Dies haben wir auf der vorigen Seite ausführlich erklärt. Beispiel:
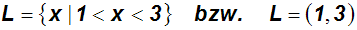
Es besteht aber noch eine dritte
Möglichkeit, nämlich eine weitere Mengenschreibweise.
Bei dieser wird die Ungleichung 1<x<3 in zwei Ungleichungen aufgeteilt,
wobei die
Elemente der Lösungsmenge die erste und die zweite
Ungleichung erfüllen müssen:
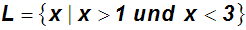
In dieser Formel kann man das Wort "und" durch das UND-Zeichen ersetzen,
dass wir aus dem Kurs
Aussagenlogik kennen:
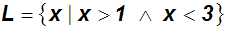
Man kann aber sagen, dass diese Art
der Darstellung der Lösungsmenge
unübersichtlicher ist. |
|
|
|