Grafischer Beweis zu:
Multiplikation und
Division mit einer
Zahl kleiner Null |
 |
Worum geht es |
|
Wir wollen beweisen, dass man das Ungleichheitszeichen umdrehen muß,
wenn man eine Ungleichung mit einer negativen Zahl mulipliziert.
Die Division mit einer negativen Zahl brauchen wir übrigens nicht
untersuchen, denn
der Division durch eine Zahl b entspricht die Multiplikation mit dem
Kehrwert 1/b.
|
 |
Beweis |
|
Multipliziert man die Zahlen der x-Achse mit einer negativen Zahl a,
so
entspricht dem Anwenden der Funktion f(x)=ax. Das Ergebnis sind dann
die Zahlen auf der y-Achse.
Im Beispiel wollen wir die Zahlen auf der x-Achse der Einfachheit halber
mit –1 multiplizieren,
was dem Anwenden der Funktion f(x) = –1x entspricht. Im Bild wird die
Zahl 3 zu –3:
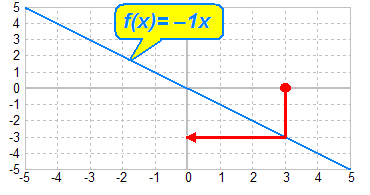
Wir wissen nun, wie man die Multiplikation von Zahlen mit einer negativen Zahl
(hier: –1)
grafisch darstellt. Daher können wir uns nun überlegen, wie sich die
Multiplikation mit einer negativen Zahl auf eine Ungleichung
auswirkt.
Nehmen wir an, dass a=2 und b=4, d.h. es gilt a < b. Jetzt
multiplizieren wir
sowohl a als auch b mit –1. Dies entspricht, wie wir gerade gelernt
haben,
dem Anwenden der Funktion f(x) = –1x:
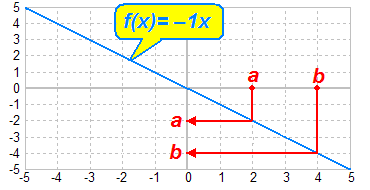
Wir sehen: Aus a<b wurde (durch die Multiplikation mit einer negativen
Zahl) a>b.
Mit anderen Worten: Wir müssen das Ungleichheitszeichen umdrehen, und
damit
ist der Satz bewiesen.
|
| |
|