|
Termumformungen |
 |
Motivation |
|
Wir haben bereits gezeigt, in welchen Fällen die Grundrechenarten
eine
Äquivalenzumformung für Ungleichungen darstellen. Beispielsweise ist die
Addition der
Zahl 3 auf beiden Seiten der Ungleichung eine Äquivalenzumformung:
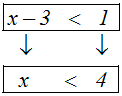
Neben den Grundrechenarten gibt es bei Ungleichungen (und Gleichungen)
aber noch weitere Rechenoperationen, die eine Äquivalenzumformung
darstellen,
z.B. die sogenannten Termumformungen. Bei Termumformungen wird
nur eine Seite
der Ungleichung geändert, und zwar durch Anwendung von
Rechengesetzen (Klammerregeln, Gesetze der Bruchrechnung, Potenzgesetze
usw.)
Beispiel:
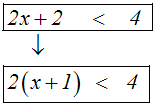
Weil
durch die Anwendung der Klammerregel ein gleichwertiger Term entsteht,
bleibt die Lösungsmenge der
Ungleichung selbstverständlich unverändert.
Termumformungen sind somit immer auch Äquivalenzumformungen.
|
| |
 |
Weitere Termumformungen |
|
Auch das Anwenden von Betragsgesetzen stellt eine Termumformung und somit
eine Äquivalenzumformung dar. Beispiel:
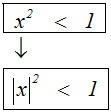
Hier wurde der Term auf der linken Seite durch eine Termumformung
verändert,
die wir im Kurs
Beträge
(neues Fenster) kennengelernt haben. |
|