Funktion und
Umkehrfunktion
heben sich auf |
 |
Erklärung |
|
Wir erklären das prinzipielle Lösen einer Ungleichung, in der Funktionen
auftreten
(Potenzfunktion, Wurzelfunktion, Logarithmusfunktion,
Exponentialfunktion usw.)
an einem Beispiel. Gegeben ist die Ungleichung:
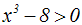
Wir isolieren die Potenz, indem wir auf beiden Seiten der Ungleichung 8
addieren.
Im Kapitel 2 haben wir gelernt, dass dies eine Äquivalenzumformung ist:
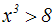
Um nun die Potenzfunktion zu beseitigen (wir wollen ja, dass x alleine
steht), müssen
wir die Umkehrfunktion anwenden, d.h. beide Seiten der Ungleichung zum
Argument
der Umkehrfunktion machen. Die Umkehrfunktion ist die
Kubikwurzelfunktion:
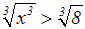
Auf der linken Seite heben sich die Potenzfunktion und ihre
Umkehrfunktion
(d.h. die Wurzelfunktion) gegenseitig auf, sodass nur noch x
übrigbleibt. Die
rechte Seite der Ungleichung kann man ausrechnen:
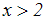
Das Beispiel diente nur zur Erklärung, wie man mit der Umkehrfunktion
eine
Ungleichung lösen kann. Auf eine mathematische Ungenauigkeit werden wir
später nochmals eingehen.
|
 |
Allgemeines Lösungs-Schema |
|
Wir fassen den Lösungsweg in Form eines Schemas zusammen:
 |
| |
|
|