|
Teilfunktion anwenden |
 |
Satz |
|
Neben einer streng montonen Funktion darf man auch eine
nicht streng monotone Funktion anwenden, wenn man nur
den streng montonen Teil der Funktion anwendet.
Dabei muss die Nebenbedingung angegeben werden, und
gegebenenfalls das Ungleichheitszeichen umgedreht werden. |
|
| |
 |
Beispiel 1 |
|
Gegeben ist folgende Wurzelungleichung mit dem Definitionsbereich R+
:
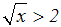
Jetzt wollen wir die Funktion quadrieren, um die Wurzel zu beseitigen.
Quadrieren ist aber leider keine
Äquivalenzumformung für Ungleichungen, weil die
Quadratfunktion weder
streng monton steigend noch streng monton fallenend ist:
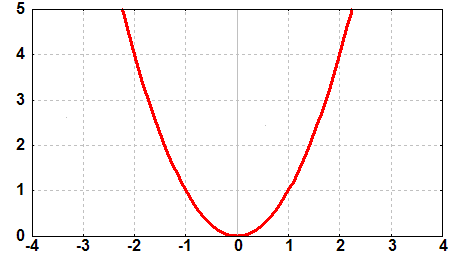
Glücklicherweise sind aber beide Seiten der gegebenen Ungleichung
nicht-negativ
(die linke Seite ist nicht-negativ, weil eine Wurzel stets
nicht-negative Werte hat).
Daher benutzen wir beim Quadrieren nur den streng-monoton-steigenden
Teil
der Quadratfunktion (x≥0), und dies
ist eine Äquivalenzumformung:
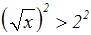
Wir vereinfachen die Ungleichung (linke Seite ein Wurzelgesetz anwenden)
und erhalten:
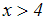
Dies ist auch die Lösung der gegebenen Ungleichung, da wir ja nur
Äquivalenzumformungen
vorgenommen haben, und die Lösungen im Definitionsbereich liegen. |
| |
 |
Beispiel 2: Streng monoton
fallenden Teil anwenden |
|
Manchmal muss man auch den "streng-monoton-fallenden" Teil der Funktion
anwenden.
Wie im Satz oben erwähnt, muss man dabei das Ungleichheitszeichen umzudrehen:
Gegeben ist folgende Wurzelungleichung mit dem Definitionsbereich R+
:
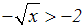
Hier sind beide Seiten der Gleichung nicht-positiv (die linke Seite ist
nicht-positiv, weil
eine Wurzel stets nicht-negativ ist, und das "Minus" das nicht-negative
Vorzeichen umdreht).
Wir quadrieren beide Seiten der Ungleichung. Dabei wird nur der negative
Teil der
Quadratfunktion benutzt, also der streng monoton fallende Teil. Folglich
müssen
wir das Ungleichheitszeichen umdrehen, sonst wäre es keine
Äquivalenzumformung:
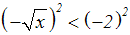
Wir vereinfachen die Ungleichung mit Hilfe der Wurzelgesetze:
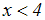
Das Quadrieren war zwar eine Äquivalenzumformung, jedoch hat sich durch
das
Anwenden des Wurzelgesetzes der Definitionsbereich vergrößert. Die
Lösungsmenge
besteht also aus der Schnittmenge des Ergebnisses und der
Definitionsmenge:
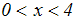
Anmerkung:
Praktisch würde man natürlich anders vorgehen. Man würde die Gleichung zuerst mit
–1
multiplizieren, dann wären beide Seiten positiv. |
| |
|