Anwenden einer
nicht
streng monotonen
Funktion |
 |
Satz |
|
Eine Funktion, die nicht streng monoton ist, darf man nicht
anwenden
(z.B. Quadratfunktion),
denn dies wäre keine Äquivalenzumformung.
Ist man gezwungen eine solche Funktion anzuwenden,
dann helfen oft "Tricks" weiter. |
|
| |
 |
Erklärung |
|
Wir haben am Anfang des Kapitels gelernt, dass das Anwenden einer streng
monotonen
Funktion eine Äquivalenzumformung für Ungleichungen darstellt (wobei man
bei
streng monoton fallenden Funktionen das
Ungleichheitszeichen umdrehen muss).
Was ist nun aber mit Funktionen, die nicht streng monoton sind?
Das beste Beispiel dafür ist die Quadratfunktion bzw. das Quadrieren:
Im Falle einer Gleichung, so hatten wir gelernt, ist
das Anwenden der Quadratfunktion
eine Folgeumformung, bei der zwar Lösungen hinzukommen
können, aber man
kann diese durch die "Probe" erkennen.
Im Falle einer Ungleichung ist das Anwendung einer
nicht streng monotonen Funktion
total verboten, da nicht nur Lösungen hinzukommen
können, sondern auch
Lösungen verloren gehen können (Beispiele siehe unten)!
Weil man aber beim Lösen von Wurzelgleichungen gezwungen ist, die
Quadratfunktion
(allgemeiner: Potenzfunktionen mit geradem Exponent) anzuwenden, zeigen
wir auf
der nächsten Seite einen "Trick", mit dem man eine
nicht streng
montone Funktion
(wie die Quadratfunktion) meist doch noch anwenden
kann.
|
| |
 |
Beispiel: Lösungen gehen
verloren |
|
Gegeben ist die Wurzel-Ungleichung:
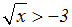
Wir quadrieren beide Seiten der Gleichung, um die Wurzel zu beseitigen:
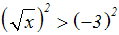
Wir vereinfachen die linke Seite, indem wir ein Wurzelgesetz anwenden:
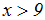
Wir sehen: Während die erste Ungleichung alle nicht-negativen Zahlen als
Lösung hat,
hat die letzte Gleichung nur noch die Zahlen als Lösung, die größer als
9 sind.
Es sind also Lösungen verloren gegangen, nämlich alle Zahlen zwischen 0
und 9. |
| |
 |
Beispiel: Lösungen kommen
hinzu |
|
Gegeben ist die Wurzel-Ungleichung:
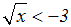
Wir quadrieren beide Seiten der Ungleichung:
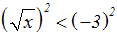
Wir vereinfachen die linke Seite, indem wir ein Wurzelgesetz anwenden:
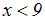
Wir sehen: Die erste Ungleichung hat kein Lösung, denn ein Wurzel kann
nicht kleiner
als eine negative Zahl werden, denn Wurzeln sind stets nicht-negativ.
Die letzte Ungleichung
hat aber Lösungen. Es sind also Lösungen hinzugekommen. |
|
|
|