Trick beim Anwenden
der Teilfunktion:
Definitionsbereich
hilft bei Bestimmung
des Vorzeichens der
Terme |
 |
Satz |
|
Bestimmt man den Definitionsbereich einer Ungleichung, so
hilft dies
oft dabei zu berechnen, welches Vorzeichen die Terme auf beiden
Seiten der Ungleichung haben. |
|
| |
 |
Erklärung am Beispiel |
|
Auf der vorigen Seite haben wir gezeigt, dass man eine Ungleichung
quadrieren darf,
wenn die Terme auf den beiden Seiten der Gleichung positiv sind. Leider
gibt es auch
Terme, deren Vorzeichen unbekannt ist.
Im Beispiel ist unbekannt, ob
die rechte Seite
der Ungleichung positiv oder negativ ist:
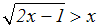
Um dieses Problem zu lösen, bestimmen wir zunächst den
Definitionsbereich der Ungleichung:

Für alle Zahlen aus dem Definitionsbereich ist die rechte Seite der
ursprünglichen
Ungleichung aber positiv. Wir dürfen die Ungleichung daher quadrieren:
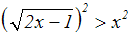
Auf der linken Seite wenden wir ein Wurzelgesetz an:
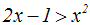
Wir bringen alle Summanden auf die rechte Seite:
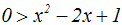
Hier liegt das 2.Binom vor, und wir können vereinfachen:
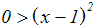
Die Lösung dieser Ungleichung ist leicht: Weil ein Quadrat nie
kleiner als Null werden kann (Quadrate von Termen sind immer
nicht-negativ), ist die Lösungsmenge die leere Menge. |
| |
|