Fälle, in denen eine
Fallunterscheidung
nötig ist |
 |
Satz |
|
Kann man bei einer Ungleichung das Vorzeichen einer Seite
nicht
(mit Hilfe des Definitionsbereiches) bestimmen, so muss man eine
Fallunterscheidung machen. |
|
| |
 |
Erklärung am Beispiel |
|
Auf der vorigen Seite wollten wir beide Seiten einer Gleichung
quadrieren, und haben in
diesem Zusammenhang dasVorzeichen der rechten Seite mit Hilfe des
Definitonsbereiches
bestimmt. Weil der Definitonsbereich positiv war, war auch die rechte
Seite stets positiv:
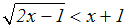
Nun betrachten wir ein Beispiel, bei dem es uns nicht hilft, den
Definitionsbereich
der Ungleichung zu untersuchen:
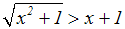
Der Definitonsbereich ist hier gleich R (wenn R die Grundmenge ist). Je
nachdem,
welche Zahl ich für x auf der rechten Seite einsetze (z.B. –10 und 10),
kann die
rechte Seite positiv oder negativ werden.
Wir müssen daher eine Fallunterscheidung durchführen. Wir nehmen einmal
an,
dass die rechte Seite der Gleichung (x+1) positiv ist, und im Fall 2,
dass sie negativ ist:

Die Lösung der Wurzelgleichung besteht aus den Lösungen der beiden
Fälle, also
aus der Vereinigungsmenge beider Fälle: L={x|x<0} |
| |
|