Wann ist eine
Teilmenge ein
Erzeugenden-
system |
 Satz
Nun stellt sich die Frage, welche Teilmengen der Vektoren
der Ebene auch Erzeugendensystem sind. Es gilt der Satz: Satz
Nun stellt sich die Frage, welche Teilmengen der Vektoren
der Ebene auch Erzeugendensystem sind. Es gilt der Satz:
Eine Teilmenge {a,b, ...} aus
Vektoren der Ebene ist ein
Erzeugendensystem der Ebene, wenn es in der Menge
mindestens ein paar linear unabhängiger Vekoren gibt. |
 Beispiele zum Satz Beispiele zum Satz
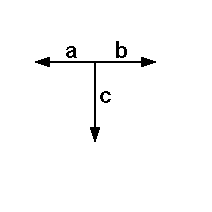 Wenn die Menge {a,b,c} ein Erzeugenden-
system der Ebene sein soll, dann muß es laut
dem obigen Satz mindestens ein paar linear
unabhängiger Vektoren in ihr geben. Es gibt
sogar zwei Paare linear unabhängiger
Vektoren in der Menge {a,b,c}, nämlich
{a,c} und {b,c}. Somit ist die Menge {a,b,c}
ein Erzeugendensystem der Ebene. Wenn die Menge {a,b,c} ein Erzeugenden-
system der Ebene sein soll, dann muß es laut
dem obigen Satz mindestens ein paar linear
unabhängiger Vektoren in ihr geben. Es gibt
sogar zwei Paare linear unabhängiger
Vektoren in der Menge {a,b,c}, nämlich
{a,c} und {b,c}. Somit ist die Menge {a,b,c}
ein Erzeugendensystem der Ebene.
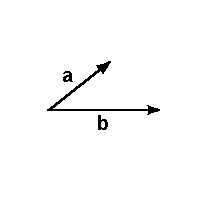 In der Menge {a,b} gibt ist ein Paar
linear unabhängiger Vektoren, besser
gesagt die Menge {a,b} selbst ist ein
Paar aus linear unabhängigen Vektoren.
Somit ist die Menge {a,b} ein Erzeugenden-
system der Ebene. In der Menge {a,b} gibt ist ein Paar
linear unabhängiger Vektoren, besser
gesagt die Menge {a,b} selbst ist ein
Paar aus linear unabhängigen Vektoren.
Somit ist die Menge {a,b} ein Erzeugenden-
system der Ebene.
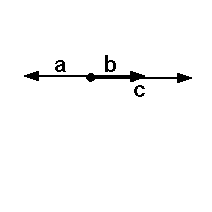 In der Menge {a,b,c} gibt es kein Paar
das linear unabhängig ist. Somit ist die
Menge {a,b,c} kein Erzeugenden-
system der Ebene. In der Menge {a,b,c} gibt es kein Paar
das linear unabhängig ist. Somit ist die
Menge {a,b,c} kein Erzeugenden-
system der Ebene.
|