Satz
Bis jetzt haben wir in diesem Kapitel Erzeugendensysteme
und Basen kennengelernt, wobei wir die Basen als linear
unabhängige Erzeugendensysteme definiert hatten.
Nun fragt man sich, was der Vorteil einer Basis gegenüber
einen Erzeugendensystem ist:
Stellt man einen Vektor x durch ein
Erzeugendensystem
dar, so ist die Darstellung in der Regel nicht eindeutig.
Das ist bei einer Basis anders:
Stellt man dagegen einen Vektor x durch eine Basis dar,
so ist die Darstellung eindeutig, d.h. es gibt nur eine
Linearkombination der Basisvektoren {a,b} , die den
Vektor x darstellt.
Beispiel zum Satz
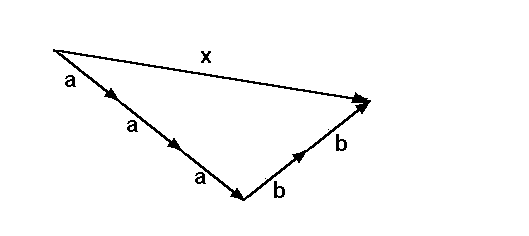
Gegeben sei die Basis {a,b} und der Vektor x.
Der Vektor x ist durch die Linearkombination 3a+2b
dargestellt:
Nun kann man keine weitere Linearkombination der Basis-
vektoren a und b finden, die ebenfalls den Vektor x
darstellt.
Satz
Bis jetzt haben wir in diesem Kapitel Erzeugendensysteme
und Basen kennengelernt, wobei wir die Basen als linear
unabhängige Erzeugendensysteme definiert hatten.
Nun fragt man sich, was der Vorteil einer Basis gegenüber
einen Erzeugendensystem ist: 
Nun kann man keine weitere Linearkombination der Basis-
vektoren a und b finden, die ebenfalls den Vektor x
darstellt.