Beweis zu:
Erzeugenden-
system der
Ebene |
 Einführung
Nun wollen wir den Satz der vorigen Seite beweisen.
Der Satz lautete: Einführung
Nun wollen wir den Satz der vorigen Seite beweisen.
Der Satz lautete:
Eine Teilmenge {a,b, ...} aus
Vektoren der Ebene ist ein
Erzeugendensystem der Ebene, wenn es in der Menge
mindestens ein paar linear unabhängiger Vekoren gibt. |
 Beweis des Satzes
Nehmen wir an, das Paar {a,b} sei ein linear unabhängiges Paar,
und x sei ein beliebiger Vektor der Ebene. Die Menge {a,b,x}
wiederum ist linear abhängig, weil drei Vektoren der Ebene
immer linear abhängig sind. Zu einer linear abhängigen Menge
kann man aber eine nichttriviale Nullsumme angeben:
k1·a + k2·b + k3·x = 0
wobei "nichttrivial" bedeutet, daß mindestens ein Koeffizient
ungleich 0 ist. Nun beweisen wir, daß auf jeden Fall k3
ungleich 0 ist:
Der Koeffizient k3 kann nicht Null sein, denn dann gelte:
k1·a + k2·b = 0
Die Vektoren a und b sind aber linear unabhängig, und
können keine nichttriviale Nullsumme bilden. Folglich gilt:
k1·a + k2·b + k3·x = 0 mit: k3 Beweis des Satzes
Nehmen wir an, das Paar {a,b} sei ein linear unabhängiges Paar,
und x sei ein beliebiger Vektor der Ebene. Die Menge {a,b,x}
wiederum ist linear abhängig, weil drei Vektoren der Ebene
immer linear abhängig sind. Zu einer linear abhängigen Menge
kann man aber eine nichttriviale Nullsumme angeben:
k1·a + k2·b + k3·x = 0
wobei "nichttrivial" bedeutet, daß mindestens ein Koeffizient
ungleich 0 ist. Nun beweisen wir, daß auf jeden Fall k3
ungleich 0 ist:
Der Koeffizient k3 kann nicht Null sein, denn dann gelte:
k1·a + k2·b = 0
Die Vektoren a und b sind aber linear unabhängig, und
können keine nichttriviale Nullsumme bilden. Folglich gilt:
k1·a + k2·b + k3·x = 0 mit: k3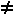 0
Weil k3 0
Weil k3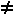 0 ist, dürfen wir die Gleichung durch k3 teilen.
Wir erhalten dann für den Vekor x:
-k1·a - k2·b
x = ---------------
k3
Weil k3 0 ist, dürfen wir die Gleichung durch k3 teilen.
Wir erhalten dann für den Vekor x:
-k1·a - k2·b
x = ---------------
k3
Weil k3 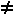 0 ist der Bruch immer definiert, und es gibt für jedes
x eine Darstellung durch eine Linearkombination von a und b. 0 ist der Bruch immer definiert, und es gibt für jedes
x eine Darstellung durch eine Linearkombination von a und b.
|