Erzeugendensysteme des Raumes
Ein Erzeugendensystem des Raumes (Anschauungsraumes)
definiert man genauso wie ein Erzeugendensystem der Ebene:
Eine Menge {a,b,c, ...} aus Vektoren
des Raumes ist ein Erzeugendensystem des Raumes, wenn man jeden Vektor
des Raumes durch eine Linearkombination der Vektoren
a, b, c, ... darstellen kann.
dies ist gleichbedeutend mit:
Liegen alle Vektoren des Raumes im
Erzeugnis <a,b,c,...> ,
so sind die Vektoren {a,b,c, ...} ein Erzeugendensystem
des Raumes.
Beispiel
Gegeben sei ein Erzeugendensystem {a,b,c,d} des Raumes:
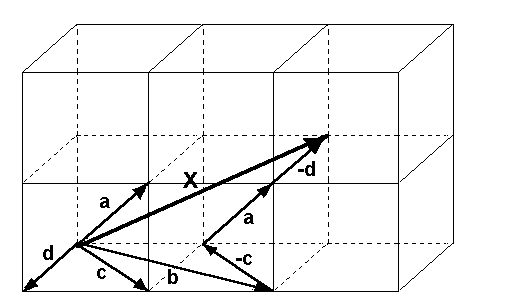
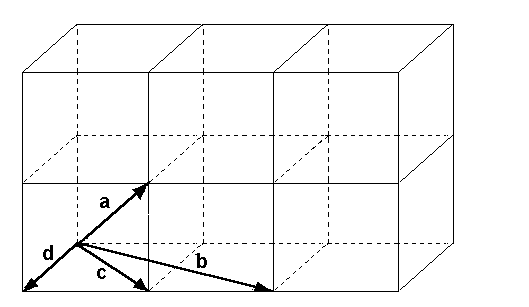dann kann ein beliebiger Vektor x kann als Linearkombination
der Vektoren {a,b,c,d}dargestellt werden: x = b - c + a - d
Erzeugendensysteme des Raumes
Ein Erzeugendensystem des Raumes (Anschauungsraumes)
definiert man genauso wie ein Erzeugendensystem der Ebene:
dann kann ein beliebiger Vektor x kann als Linearkombination
der Vektoren {a,b,c,d}dargestellt werden: x = b - c + a - d
