Wann ist eine
Menge ein
Erzeugenden-
system des
Raumes
Satz vom Erzeugendensystem
Nun stellt sich die Frage, wann eine Menge aus Vektoren des
Raumes ein Erzeugendensystem ist. Es gilt der folgende Satz:
Eine Menge {a, b, c, ...} aus
Vektoren des Raumes ist
ein Erzeugendensystem des Raumes, wenn sich in der
Menge drei linear unabhängige Vektoren finden.
Beispiel und Gegenbeispiel
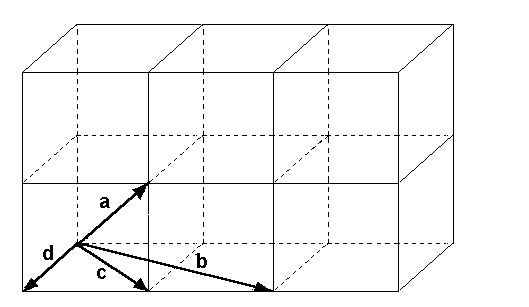
Im folgenden Bild ist die Menge M={a, b, c, d} ein
Erzeugendensystem des Raumes, weil es in der
Menge M drei linear unabhängigen Vektoren gibt,
z.B. sind die Vektoren {a,b,c} linear unabhängig:
Im folgenden Bild ist die Menge M={a, b, c, d}
kein Erzeugendensystem des Raumes, weil es in der
Menge M keine drei linear unabhängigen Vektoren gibt:
Satz vom Erzeugendensystem
Nun stellt sich die Frage, wann eine Menge aus Vektoren des
Raumes ein Erzeugendensystem ist. Es gilt der folgende Satz:
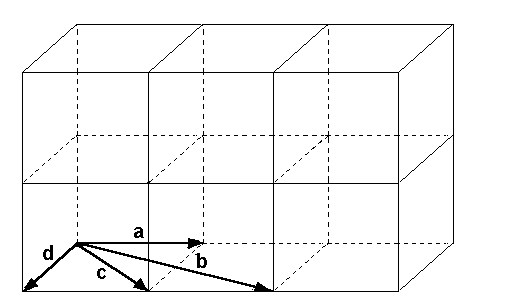
Im folgenden Bild ist die Menge M={a, b, c, d}
kein Erzeugendensystem des Raumes, weil es in der
Menge M keine drei linear unabhängigen Vektoren gibt:
