Einleitung
Auf der letzten Seiten haben wir Erzeugendensysteme des
Raumes kennengelernt. Nun wollen wir eine spezielle Art
eines Erzeugendensystemes des Raumes kennenlernen,
die man Basis des Raumes nennt:
Definition
Gegeben sei ein Erzeugendensystem des Raumes.
Sind die Vektoren dieses Erzeugendensystems auch linear unabhängig, so nennt man das Erzeugendensystem
des Raumes, eine Basis des Raumes.
Beispiel und Gegenbeispiel
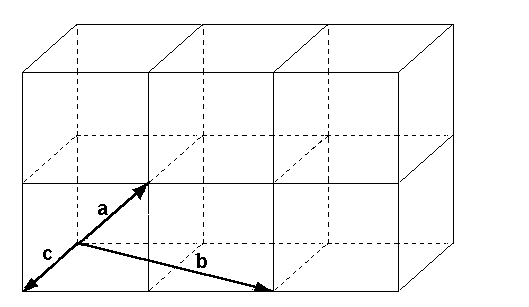
Die Vektoren a,b,c sind ein Erzeugendensystem des Raumes.
Weil die Vektoren des Erzeugendensystems auch linear
unabhängig sind, nennt man sie eine Basis des Raumes:
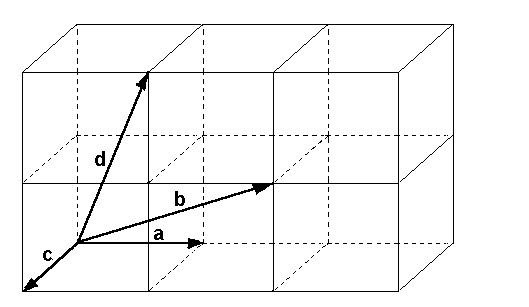
Dagegen sind die vier Vektoren a,b,c,d zwar ein Erzeugenden-
system, aber nicht linear unabhängig (4 Vektoren im Raum sind
immer linear abhängig) und bilden somit keineBasis des Raumes:
Einleitung
Auf der letzten Seiten haben wir Erzeugendensysteme des
Raumes kennengelernt. Nun wollen wir eine spezielle Art
eines Erzeugendensystemes des Raumes kennenlernen,
die man Basis des Raumes nennt:
Dagegen sind die vier Vektoren a,b,c,d zwar ein Erzeugenden-
system, aber nicht linear unabhängig (4 Vektoren im Raum sind
immer linear abhängig) und bilden somit keine Basis des Raumes:
