Unter der Dimension eines Raumes
versteht man die
Anzahl der Basisvektoren einer Basis dieses Raumes.
Erläuterung
Wir haben gesehen, daß man zur eindeutigen Darstellung eines
Vektors v der Ebene genau zwei linear unabhängige Vektoren
braucht. d.h. jede Basis der Ebene hat zwei Vektoren.
Man nennt die Ebene deshalb zweidimensional:
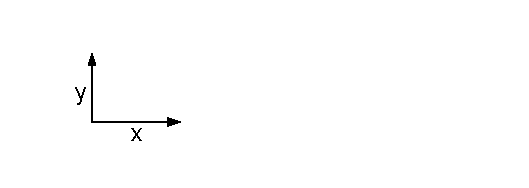Analog braucht man zur eindeutigen Darstellung eines Vektors v
des Anschauungsraumes genau drei linear unabhängige Vektoren,
d.h. jede Basis des Anschauungsraumes hat drei Vektoren.
Man nennt den Anschauungsraum deshalb dreidimensional.
Definition
Analog braucht man zur eindeutigen Darstellung eines Vektors v
des Anschauungsraumes genau drei linear unabhängige Vektoren,
d.h. jede Basis des Anschauungsraumes hat drei Vektoren.
Man nennt den Anschauungsraum deshalb dreidimensional.
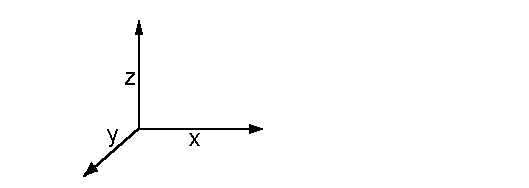
