Version: Test
©Raddy 2000

Inhalt zu: Vektoralgebra VI    ZURÜCK
Info-Seite Vorkenntnisse: ...      Themen:   ...     Infos: www.mathematik.net
Komponenten
und Koordinaten
eines Vektors		 Gegeben sei ein Vektor vekt-x.pcx (226 Byte), der als Linearkombination der
Basisvektoren vekt-a.pcx (221 Byte) und vekt-b.pcx (221 Byte) gegeben ist:

           vekt-x.pcx (226 Byte) = k1·vekt-a.pcx (221 Byte) + k2·vekt-a.pcx (221 Byte)

Dann nennt man k1·vekt-a.pcx (221 Byte) die erste Komponente und  k2·vekt-a.pcx (221 Byte)
die zweite Komponente des Vektors vekt-x.pcx (226 Byte).

k1 und k2 nennt man die erste und zweite Koordinate von x
bezüglich der Basis {vekt-a.pcx (221 Byte),vekt-b.pcx (221 Byte)}. Man schreibt die Koordinaten
untereinander und in runde Klammern:
vak6s0p1.pcx (1675 Byte)
Ortnormalbasis
und kartesische
Koordinaten 		Beziehen sich die Koordinaten auf eine rechtwinklige
Einheitsbasis (Orthonormalbasis), so nennt man die Koordinaten
kartesische Koordinaten.
Vektoraddition
in Koordinaten-
form		 Die Vektoraddition in Koordinatenform erfolgt koordinatenweise: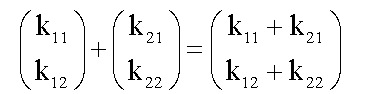
vak6s0p2.pcx (3777 Byte)
Beweis Beweis der Formel
Vektorsubtraktion
in Koordinaten-
form		 Die Vektorsubtraktion in Koordinatenform erfolgt koordinatenweise: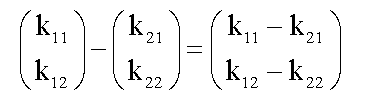
vak6s0p3.pcx (3609 Byte)
Skalare
Vervielfachung
in Koordinaten-
form		 Die skalare Vervielfachung in Koordinatenform erfolgt koordinatenweise: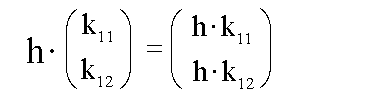
vak6s0p4.pcx (2680 Byte)
Beweis Beweis der Formel