Komponenten
und Koordinaten
eines Vektors |
 Komponenten
In den beiden vorigen Kapitel haben wir gelernt, daß man
einen beliebigen Vektor der Ebene (bzw. des Raumes)
durch eine Basis der Ebene (bzw. des Raumes) eindeutig
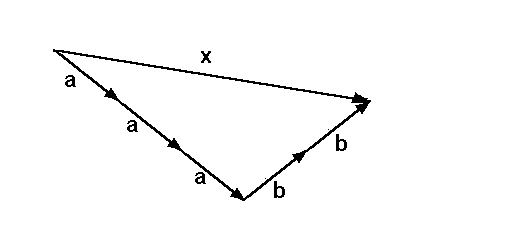
ausdrücken kann. Als Beispiel hatten wir den Vektor x
durch die Linearkombination x = 3·a + 2·b der Basis {a,b}
ausgedrückt: Komponenten
In den beiden vorigen Kapitel haben wir gelernt, daß man
einen beliebigen Vektor der Ebene (bzw. des Raumes)
durch eine Basis der Ebene (bzw. des Raumes) eindeutig
ausdrücken kann. Als Beispiel hatten wir den Vektor x
durch die Linearkombination x = 3·a + 2·b der Basis {a,b}
ausgedrückt:
 Was sind nun Komponenten?
Man nennt den Vektor 3·a die erste Komponente des
Vektors x, und den Vektor 2·b die zweite Komponente
des Vektors x.
Was sind nun Komponenten?
Man nennt den Vektor 3·a die erste Komponente des
Vektors x, und den Vektor 2·b die zweite Komponente
des Vektors x.
 Koordinaten
Wie oben erwähnt sind 3·a und 2·b die beiden Komponenten
des Vektors x. Die Zahlen 3 und 2 heißen nun die Koordinaten
des Vektors x, bezüglich der Basis {a,b}. Üblicherweise schreibt
man die Koordinaten untereinander und in runde Klammern: Koordinaten
Wie oben erwähnt sind 3·a und 2·b die beiden Komponenten
des Vektors x. Die Zahlen 3 und 2 heißen nun die Koordinaten
des Vektors x, bezüglich der Basis {a,b}. Üblicherweise schreibt
man die Koordinaten untereinander und in runde Klammern:
 Aus Platzgründen schreibt man die Koordinaten manchmal
in Zeilenform: (3,2)
Wichtig: Zu der Angabe der Koordinaten eines Vektors
gehört auch immer die Angabe der Basis, auf
welche sich die Koordinaten beziehen.
Aus Platzgründen schreibt man die Koordinaten manchmal
in Zeilenform: (3,2)
Wichtig: Zu der Angabe der Koordinaten eines Vektors
gehört auch immer die Angabe der Basis, auf
welche sich die Koordinaten beziehen.
|