Skalare
Vervielfachung
in Koordinaten-
form |
 Skalare Vervielfachung in Koordinatenform
Die Skalare Vervielfachung eines Vektors wird genauso wie
die Vektoraddition und die Vektorsubtraktion
koordinatenweise durchgeführt:
Gegeben sei ein Skalar und ein Vektor in Koordinatenform.
Das Produkt aus Skalar und Vektor wird gebildet, indem
man jede Koordinate des Vektors mit dem Skalar multipliziert: Skalare Vervielfachung in Koordinatenform
Die Skalare Vervielfachung eines Vektors wird genauso wie
die Vektoraddition und die Vektorsubtraktion
koordinatenweise durchgeführt:
Gegeben sei ein Skalar und ein Vektor in Koordinatenform.
Das Produkt aus Skalar und Vektor wird gebildet, indem
man jede Koordinate des Vektors mit dem Skalar multipliziert:
 Beweis
folgt auch nächster Seite. Zunächst ein Beispiel: Beweis
folgt auch nächster Seite. Zunächst ein Beispiel:
 Beispiel
Gegeben sei ein Skalar und ein Vektor in Koordinatendarstellung,
aus denen das Skalare Vielfache gebildet werden soll: Beispiel
Gegeben sei ein Skalar und ein Vektor in Koordinatendarstellung,
aus denen das Skalare Vielfache gebildet werden soll:
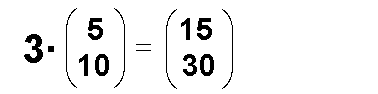 Wie in der Definition gesagt, wird das Skalare Vielfache
koordinatenweise gebildet. Wir multiplizieren also jede
Koordinate mit dem Skalar:
Wie in der Definition gesagt, wird das Skalare Vielfache
koordinatenweise gebildet. Wir multiplizieren also jede
Koordinate mit dem Skalar:
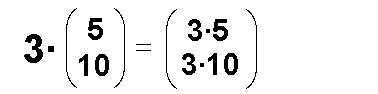 Das Ergebnis lautet somit:
Das Ergebnis lautet somit:
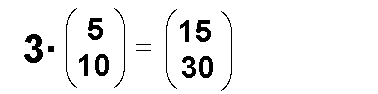
|