Beweis der
Formel:
Vektoraddition
in Koordinaten-
form |
 Beweis
Nun wollen wir die Formel (von der vorigen Seite) für die
Vektoraddition in Koordinatendarstellung beweisen.
Die Formel lautete: Beweis
Nun wollen wir die Formel (von der vorigen Seite) für die
Vektoraddition in Koordinatendarstellung beweisen.
Die Formel lautete:
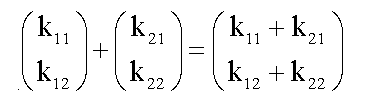 Zuerst wechseln wir von der Koordinatenform in die
Komponentenform:
Zuerst wechseln wir von der Koordinatenform in die
Komponentenform:
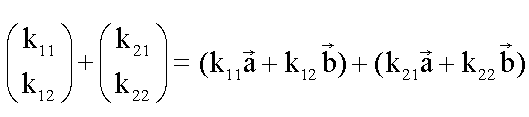 Wir wissen: Für die Vektoraddition gilt das Assoziativgesetz.
Deshalb dürfen wir die Formel auch so schreiben:
Wir wissen: Für die Vektoraddition gilt das Assoziativgesetz.
Deshalb dürfen wir die Formel auch so schreiben:
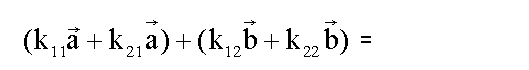 Auf diese Formel wenden wir das Distributivgesetz der
skalaren Vervielfachung an:
Auf diese Formel wenden wir das Distributivgesetz der
skalaren Vervielfachung an:
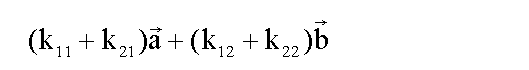 Dies ist die Komponentenform eines Vektors, den wir nun
wieder in Koordinatenform schreiben:
Dies ist die Komponentenform eines Vektors, den wir nun
wieder in Koordinatenform schreiben:
 Damit haben wir die Formel bewiesen.
Damit haben wir die Formel bewiesen.
|