Wurzelungleichungen
löste man durch
Potenzieren |
 |
Erklärung |
|
Beim Lösen von Wurzelungleichungen durch Äquivalenzumformungen
muß man viele Feinheiten beachten, auf die wir im Laufe des Kapitels
eingehen werden.
Grundsätzlich werden Wurzelungleichungen durch Potenzieren gelöst.
Wir werden uns daher im Verlauf des Kapitels fragen müssen, wann
potenzieren überhaupt eine Äquivalenzumformung ist.
|
 |
Beispiel |
|
Das Beispiel soll nur einen groben Überblick liefern. Auf die
Feinheiten und
Fallstricke
gehen wir - wie gesagt - im Laufe des Kapitels ein.
Gegeben ist die Wurzelungleichung:
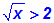
Wir bestimmen den Definitonsbereich:
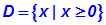
Wir potenzieren beide Seiten mit dem Wurzelexpoenten, also hier mit 2:
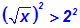
Auf der linken Seite benutzen wir das Wurzelgesetz
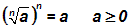
und erhalten dadurch:

Alle Lösungen liegen im Definitionsbereich. Daher gilt:
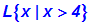
Sprich: Die Lösungsmenge besteht aus den Elementen x, für die gilt, x
ist größer als 4. |
|