Bei Wurzelungleichungen
der Form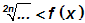 
sind beide Seiten
nicht-negativ |
 |
Satz |
|
Bei Wurzelungleichungen der Form
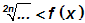sind beide
Seiten nicht-negativ,
und das "Potenzieren der Ungleichung mit einer geraden Zahl" ist
daher
eine Äquivalenzumformung. |
|
|
|
Erklärung |
|
Wir haben zu Anfang des Abschnitts gelernt, dass man eine
Wurzelungleichung
mit einer geraden Zahl potenzieren darf, wenn beide Seiten der
Ungleichung
nicht-negativ sind.
Bei manchen Wurzelungleichungen kann man nicht sofort erkennen, ob beide
Seiten
der Ungleichung nicht-negativ sind, z.b. bei Ungleichungen der Form:
.
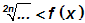Als Beispiel betrachten wir die Ungleichung:
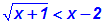
Hier hilft eine kleine Überlegung weiter: Die linke Seite ist
nicht-negativ,
denn Wurzeln haben immer einen nicht-negativen Wert. Aufgrund des
Ungleichheitszeichens muß die rechte Seite aber größer als die linke
sein,
und daher ist auch die rechte Seite nicht-negativ.
Und weil beide Seiten nicht-negativ sind, dürfen wir die Ungleichung
potenzieren.
|
|