|
Am Anfang dieses Kapitels hatten wir den Begriff
der Wurzel x definiert als Lösung der Gleichung xn=a:
Dabei hatten wir folgende drei Einschränkungen getroffen:
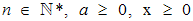
Auf dieser Seite wollen wir erklären, warum wir nur nicht-negative x
zulassen.
Dazu betrachten wir den Wert x einer Wurzel mit geradem Wurzelexponenten:

Laut der Wurzel-Definiton ist diese Wurzel x die Lösung von x2=9:
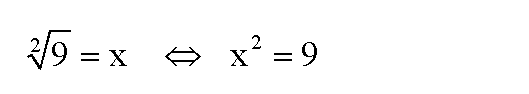
Die rechte Gleichung hat nun aber zwei Lösungen ( +3 und -3)
und somit hätte auch die Wurzel x zwei Lösungen +3 und -3).
Dadurch wäre eine
Wurzel aber ein zweideutiger Rechenausdruck.
Doch es kommt noch
schlimmer: Eine Addition dreier Wurzeln könnte dadurch
sogar acht Lösungen haben. Beispiel:
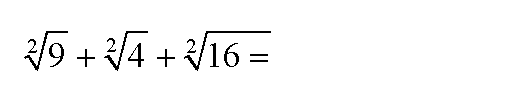
(Lösungen wären z.B. 3+2+4 oder 3-2+4 oder 3-2-4 oder ...)
Um solche Mehrdeutigkeiten zu vermeiden, legt man daher fest:
|