|
Wir betrachten eine Wurzel mit geraden
Wurzelexponent:

Laut Definition der Wurzel ist die Wurzel die Lösung der zugehörigen Potenzgleichung:
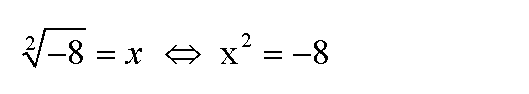
Doch egal welche Zahl man für x in die rechte
Gleichung einsetzt,
es kommt niemals -8 heraus, denn wenn eine Zahl mit 2 potenziert
wird, kommt immer eine positive Zahl heraus, nie eine negative!
Folglich hat auch die Wurzel keine Lösung.
Bei negativen Radikanden hat eine Wurzel also manchmal keine
Lösung, und deshalb läßt man keine negativen Radikanden zu. |
|
Nun könnte man auf die Idee kommen, zumindest
für ungerade Wurzelexponenten
einen negativen Radikanden zuzulassen, denn die zugehörige
Potenzgleichung hat
im Fall eines ungeradem Exponenten immer eine Lösung
(hier: –2):
Hier müssen wir nun anmerken,
dass es zwischen den Mathematikern einen Streit gibt:
Die eine Hälfte der Mathematiker ist der Meinung, dass eine Wurzel mit
ungeraden
Wurzelexponenten (hier: 3) und negativen Radikanden (hier: –8)
nicht definiert ist.
Auch wir sind dieser Meinung, nicht zuletzt, weil dies in der
DIN1302 gesetzlich
so festgelegt worden ist (DIN = Deutsche Industrie Norm)!
Ein Begründung der DIN geben wir am Ende von Kapitel 2. Für Profis
vorab:
Bei negativen Radikanden könnte man unsinnige Aussagen beweisen,
wie –2=2:
Die andere Hälfte der
Mathematiker (besonders alle Schulbuch-Autoren in den USA)
machen es sich ganz leicht: Sie definieren einfach:
Wie gesagt werden wir am Ende von Kapitel 2 näher darauf eingehen,
denn um das Problem
zu verstehen, müssen wir erst die Wurzelgesetze kennenlernen. |