Radizieren als
Umkehrung des
Potenzieren |
 |
Einleitung |
|
Auf den vorigen Seiten haben wir gelernt: Potenzieren
ist die
Umkehrung des Radizierens.
Nun wollen wir zeigen, daß auch
die
Umkehrung dieser Aussage gilt:
Radizieren (Wurzelziehen) ist die Umkehrung des Potenzierens. |
 |
Formel |
|
Wir betrachten die Gleichung:
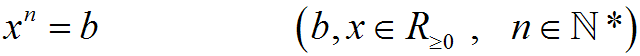
Laut der Definition der Wurzel ist folgende Schreibweise
äquivalent (gleichwertig):
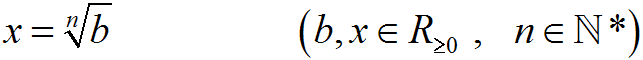
Nun ersetzen wir in der zweiten Gleichung die Formvariable b
durch den Wert von "b" in der ersten Gleichung:
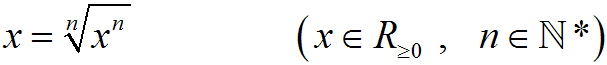
Um später eine andere Formel leichter herleiten zu können, führen
wir hier noch eine Umbenennug durch: Die Variable x nennen a:
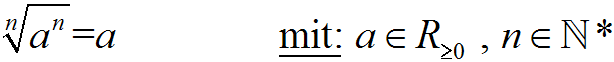
Nun erklären wir die Bedeutung dieser Formel: |
 |
Radizieren als Umkehrung des Potenzierens |
|
Die Formel sagt uns: Wenn wir die Zahl a mit n
potenzieren
und aus dem Ergebnis die n-te Wurzel aus dem Ergebnis ziehen,
dann erhalten wir wieder die Zahl a.
Das Radizieren hebt also das Potenzieren wieder auf, d.h.
Radizieren und Potenzieren sind umgekehrte Rechnenoperationen,
so wie Addieren das Subtrahieren aufhebt (Beispiel: a–3+3=a) |
 |
Einschränkung der Formel |
|
Man beachte, daß wir beim Beweis der Formel
vorausgesetzt haben,
daß a nicht-negativ ist. Auf der übernächsten Seite werden wir untersuchen,
was passiert, wenn wir diese Einschränkung fallen lassen. |
|