Häufiger Fehler
bei der Anwendung
und Erweiterung
des Satzes:
Radizieren als
Umkehrung des
Potenzieren |
 |
Gerader Wurzelexponent |
|
Wir haben gerade einen Satz
kennen gelernt, der sagte, dass eine Potenzierung mit n
durch eine Radizierung mit n wieder aufgehoben wird. Als Formel:
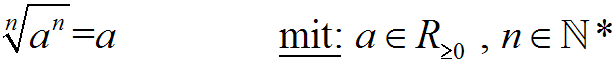
Wie man lesen kann, ist diese Formel nur gültig, wenn a nicht-negativ
ist.
Der Grund für diese Einschränkung ist der folgende Fall:
Wenn der Wurzelexponent gerade ist und wenn a negativ ist,
dann heben sich Potenzieren und Radizieren nicht auf. Im Beispiel hebt
sich das Quadrieren und Radizieren von –3 nicht auf:

Es ändert sich nämlich das Vorzeichen von –3, und es gilt stattdessen:

Wenn wir bei geradem Wurzelexponenten (2n) auch negative a
zulassen wollen,
müssen wir
somit eine Fallunterscheidung machen, oder einfach den Betrag bilden:
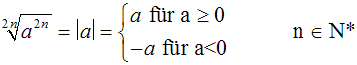
 |
 |
Ungerader Wurzelexponent |
|
Bei ungeradem Wurzelexponenten (hier: 3) und positiven a
(hier: a=7) heben sich Potenzieren und Radizieren gegenseitig auf, wie
wir schon auf der vorigen Seite erklärt haben:
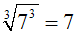
Wenn aber a negativ ist (hier: –5), dann ist die Wurzel nicht definiert,
weil der Radikand negativ ist:
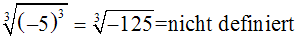 |
 |
Zusammenfassung beider Fälle
und Beispiele |
|
Wir können nun für beide Fälle
(gerader/ungerader Wurzelexponent) eine erweiterte
Formel angeben, bei der für gerade Exponenten auch negative a
zugelassen werden:
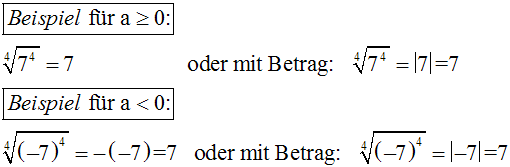
Beispiele zu allen vier
möglichen Fällen:
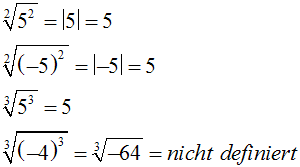 |
|