Beweis:
Kürzen und
Erweitern
des Wurzel-
exponenten |
 |
Beweis |
|
Wir wollen folgenden Satz beweisen:
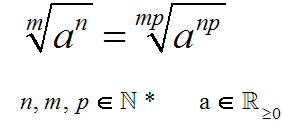
Um den Satz zu beweisen, schreiben die linke Seite der Gleichung
nochmal auf, und versuchen sie mit Hilfe der Wurzelgesetze
in die rechte Seite umzuformen:
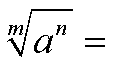
Im Kapitel 1 haben wir den Satz gelernt, daß Radizieren
und Potenzieren sich aufheben, wenn der Exponent (hier: p)
gleich ist:
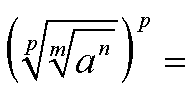
Nun wenden wir den Satz über das Radizieren von
Wurzeln an, den wir in diesem Kapitel gelernt haben:
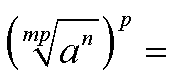
Wir wenden den Satz über das
Potenzieren von Wurzeln an, den wir ebenfalls
in diesem Kapitel kenngelernt haben: Statt eine Wurzel (mit p)
zu potenzieren,
darf man den Radikanden (mit p) potenzieren:
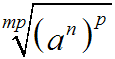
Jetzt wenden wir auf den Radikanden einen Satz aus der Potenzrechnung
an,
nämlich den Satz über das "Potenzieren einer Potenz": Man potenziert
eine
Potenz an mit p, indem man den die Exponenten (n und p)
multipliziert:
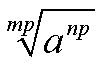
Damit haben wir die linke Seite der Gleichung in die rechte
Seite umgeformt, und somit ist der Satz bewiesen.© by www.mathematik.net |
|