Anwendung:
Warum laut DIN 1302 negative Radikanden verboten sind |
 |
Erklärung |
|
Im ersten Kapitel haben wir
den Begriff Wurzel definiert.
Bei der Definition hatten wir negative Radikanden grundsätzlich
verboten, und uns auf die Deutsche Industrienorm 1302 (DIN1302)
berufen.
Wir wollen nun begünden, warum die DIN1302 negative Radikanden
verbietet. |
 |
Grund 1: Erweiterung von
Wurzeln |
|
Würde man nämlich auch
negative Radikanden (bei ungeradem
Wurzelexponent) erlauben, so würden durch die Wurzelgesetez
(z.B. "Erweitern von Wurzeln") unsinnige Aussagen entstehen.
Betrachten wir dazu ein Beispiel. Für die dritte Wurzel aus –8
ergäbe
sich der Wurzelwert –2, denn laut der Definition der Wurzel ist die
"dritte Wurzel aus –8" die Lösung der Potenzgleichung: x3=–8:
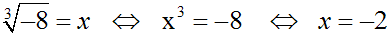
Andererseits kann man die Wurzel erweitern und dann lösen:
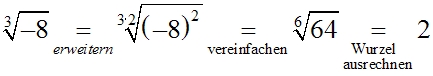
Die Wurzel hätte also zwei verschiedene Werte.
Wir hätten die unsinnige Aussage bewiesen: –2=2
|
 |
Grund 2: Potenzgesetze |
|
Es gibt einen weiteren Grund,
doch um diesen zu verstehen mußt du
das Kapitel Potenzen III durchgearbeitet haben, oder dich mit
"Potenzen mit gebrochenen Exponenten" auskennen.
Wenn wir nämlich negative Radikanden (für ungerade Wurzelexponenten)
zulassen,
dann kann man nicht mehr Wurzeln als "Potenzen mit gebrochenen
Exponenten"
definieren. Beispiel:
Wir berechnen wieder die dritte Wurzel aus –8 mit Hilfe der
Wurzel-Definition:
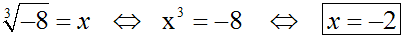
Andererseits kann man die Wurzel in eine Potenz mit gebrochenen
Exponenten umwandeln,
den Exponenten erweitern und ein Potenzgesetz anwenden, und erhält:
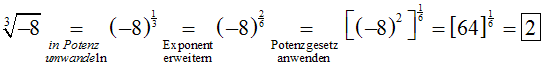
Und wieder haben wir die falsche Aussage bewiesen: –2=2
|
 |
Fazit |
|
Wenn wir negative
Radikanden (bei ungeradem Wurzelexponenten) zulassen würden,
dann würden einige Wurzel- und Potenzgesetze ungültig.
Daher ist es durchaus sinnvoll, dass die DIN 1302 negative Radikanden
verbietet. |
|