Sonderfall:
Nenner ist stets positiv |
 |
Erklärung |
|
Bevor wir versuchen eine Bruchungleichung durch eine
Fallunterscheidung zu lösen,
ist es sinnvoll zu überprüfen, ob nicht der folgende Sonderfall
vorliegt:
Der Nenner ist für alle x des
Definitionsbereiches ist
entweder stets größer Null oder aber stets kleiner als Null.
In diesem Fall ist keine Fallunterscheidung nicht, wenn wir die
Ungleichung
mit dem Nenner multiplizieren. Im ersten Fall bleibt das
Ungleichheitszeichen
erhalten, im zweiten Fall muß es umgedreht werden.
|
 |
Beispiel 1 |
|
Betrachten wir das Beispiel:
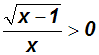
Hier besteht der Definitionsbereich aus allen Zahlen, die größer oder
gleich 1 sind,
denn nur dann ist der Radikand der Wurzel nicht-negativ und somit
definiert. Daher
dürfen wir die Ungleichung mit x multiplizieren, ohne dass eine
Fallunterscheidung nötig ist.
|
 |
Beispiel 2 |
|
Betrachten wir das Beispiel:
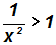
Zuerst bestimmt man den Definitionsbereich. Er besteht aus den
reellen Zahlen, abzüglich der Null:
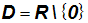
Der nächste Schritt wäre die Multiplikation mit dem Nenner, wobei
normalerweise eine Fallunterscheidung nötig wäre. Wir können uns
aber überlegen, dass der Nenner stets positiv ist:
1.Der Nenner ist nicht negativ, denn ein Quadrat ist nie
negativ,
sondern positiv oder Null.
2.Der Nenner ist nicht Null, denn dies wurde beim der
Bestimmung des Definitionsbereiches
ausgeschlossen.
Daher können wir einfach mit dem Nenner multiplizieren, d.h. ohne
eine Fallunterscheidung machen zu müssen:
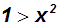
Potenzungleichungen dieser Art hatten wir schon
hier
behandelt. Man löst sie durch
Radizieren und das Anwenden eines Wurzelgesetzes:
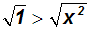
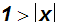
Dann löst man die entstandene Betragsungleichung, und erhält unter
Beachtung des Definitionsbereiches (drei Schreibweisen):
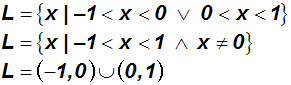
|
|