Gewinnumformungen, Verlustumformungen
und
Umformungen,
die zu undefinierten
Ausdrücken führen |
 |
Worum geht es: Unerlaubte
Umformungen |
|
Am Anfang des Kapitels haben wir die Äquivalenzumformungen für
Ungleichungen
wiederholt. Neben Äquivalenzumformungen gibt es noch drei bei
Ungleichungen nicht
erlaubte Umformungen:
1.
Gewinnumformungen
(auch Folgeumformungen genannt)
2. Verlustumformungen
3. Umformungen, die zu undefinierten Ausdrücken führenDiese drei Umformungen wurden
im Kurs
Ungleichungen erklärt.
|
 |
Gewinnumformungen bei
Ungleichungen |
|
Wir durch eine Umformung die Lösungsmenge einer Ungleichung vergrößert,
dann spricht man von einer Gewinn oder Folgeumformung.
Die falschen
Lösungen nennt man Scheinlösungen. Bei Ungleichungen
gibt es nur eine
Art von
Gewinnumformung:
Die Erweiterung des Definitionsbereiches
Bei Gleichungen kann man Scheinlösungen durch eine Probe herausfiltern,
doch bei Ungleichungen gibt es keine Probe (weil die Lösungsmenge meist
aus unendlich vielen Lösungen besteht. Daher sind
Gewinnumformungen
bei Ungleichungen verboten.
|
 |
Verlustumformungen bei
Ungleichungen |
|
Bei einer Verlustumformung gehen Lösungen verloren. Man muß daher
bei jeder
Umformung darauf achten, dass es sich nicht um eine
Verlustumformung handelt.
Bei Ungleichungen können drei Dinge
zu
einer Verlustumformung führen:
1. Einschränken des Definitionsbereiches der Funktion,
wenn Lösungen in dem Bereich liegen, der
wegfiel.
Beispiel: Gegeben ist die Ungleichung:
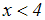
Die Lösung dieser Ungleichung sind
alle Zahlen, die kleiner als 4 sind.
Wir radizieren die Ungleichung:
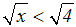
Jetzt gehören nur noch die Zahlen
zwischen Null und 4 zur Lösungsmenge,
denn für Zahlen, die kleiner als Null
sind, ist die Wurzel nicht definiert.
2. Falsches Anwenden von Rechengesetzen. Genauer:
Das Nichtbeachten des Definitionsbereichs
der Rechengesetze
3. Das Anwenden einer nicht streng monoton verlaufenden Funktion
Beispiel: Eine Ungleichung quadrieren (Quadratfunktion
anwenden)
Merke: Verlustumformungen sind natürlich ebenfalls verboten.
|
 |
Umformungen, die zu undefinierten
Ausdrücken |
|
Führt eine Umformung zu einem undefinierten Ausdruck, so handelt es sich
um eine unerlaubte Umformung. Beispiel:
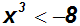
Jetzt ziehen wir die dritte Wurzel:
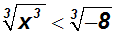
Auf der rechten Seite entsteht ein undefinierter Ausdruck, denn Wurzeln
aus
negativen Zahlen sind nicht definiert. Die Umformung ist daher nicht
erlaubt.
Merke: Umformungen, die auf undefinierte Ausdrücke führen, sind
verboten.
|
|
|
|