x² > a
(a nicht-negativ) |
 |
Lösungsweg |
|
Gegeben ist die Potenzungleichung mit geradem Exponent:
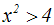
Beide Seiten der Ungleichung sind nicht-negativ, d.h. positiv oder Null
(die
linke
Seite der Ungleichung ist nicht-negativ, weil Quadrate immer
nicht-negativ sind).
Nun wollen wir auf beiden Seiten der Ungleichung die Wurzel ziehen.
Dies ist eine Äquivalenzumformung, weil beide Bedingungen für eine
Äquivalenz-
umformung vorliegen:
1. Die Wurzelfunktion ist streng monoton steigend
2. Der Definitionsbereich wird nicht
eingeschränkt, denn beide Seiten
der Ungleichung sind
positiv (gerade Potenzen sind stets positiv)
Wir erhalten:
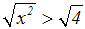
Ein häufiger Fehler ist nun, dass wir die linke Seite der Ungleichung zu
x vereinfachen.
Doch es gilt: Auf der linken Seite der Ungleichung heben sich
Potenzieren und
Radizieren nicht auf, denn die Wurzelfunktion ist
nicht die
Umkehrfunktion
der Quadratfunktion (die Quadratfunktion hat nämlich überhaupt keine
Umkehrfunktion).
Wir können aber, um die linke Seite der Ungleichung zu vereinfachen,
das folgende Wurzelgesetz anwenden: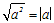 .
Wir erhalten: .
Wir erhalten:
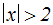
Wir lösen diese einfache
Betragsungleichung und erhalten die Lösung:
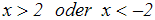 |
| |
|