|
Sonderfälle |
 |
Worum geht es |
|
Bevor wir versuchen eine Wurzelungleichung zu lösen (wie das geht
lernen wir
im Kapitel 2 und 3), sollten wir uns erstmal vergewissern, dass es sich
nicht um
einen Sonderfall handelt, den man "im Kopf" lösen kann
|
 |
Sonderfall 1 |
|
Gegeben sei eine Wurzelungleichung des folgenden Typs:

Als Beispiel betrachten wir die Wurzelungleichung:

Weil eine Wurzel - laut ihrer
Definition - immer
nicht-negativ ist (d.h. positiv oder Null),
ist sie stets größer als eine negative Zahl, und somit ist die
Wurzelungleichung
für alle x aus dem Definitionsbereich wahr.
Die Lösungsmenge L ist also gleich dem Definitionsbereich D:
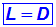
|
 |
Sonderfall 2 |
|
Gegeben sei eine Wurzelungleichung des folgenden Typs:

Als Beispiel betrachten wir die Wurzelungleichung:

Weil eine Wurzel - laut ihrer
Definition - immer
nicht-negativ ist (d.h. positiv oder Null),
ist sie stets größer oder gleich einer nicht-positiven Zahl, und somit
ist
die Wurzelungleichung für alle x aus dem Definitionsbereich wahr.
Die Lösungsmenge L ist also gleich dem Definitionsbereich D:
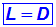
|
 |
Sonderfall 3 |
|
Gegeben sei eine Wurzelungleichung des folgenden Typs:

Als Beispiel betrachten wir die Wurzelungleichung:

Weil eine Wurzel - laut ihrer
Definition - immer
nicht-negativ ist (d.h. positiv oder Null),
kann sie nicht kleiner als die Zahl Null sein. Die Lösungsmenge L ist
also die leere Menge:

|
 |
Sonderfall 4 |
|
Gegeben sei eine Wurzelungleichung des folgenden Typs:

Als Beispiel betrachten wir die Wurzelungleichung:

Weil eine Wurzel - laut ihrer
Definition - immer
nicht-negativ ist (d.h. positiv oder Null),
kann sie nicht kleiner oder gleich der negativen Zahl –1 sein.
Die Lösungsmenge L der Ungleichung ist also die leere Menge:
 |
|