Potenzieren mit
ungeraden
Exponenten ist eine
Äquivalenzumformung |
 |
Satz |
|
Im Beispiel auf der vorigen Seite haben wir die Ungleichung einfach
potenziert,
ohne uns zu fragen, ob dies überhaupt eine Äquivalenzumformung ist. Dies
wollen wir auf dieser Seite nachholen.
Wir betrachten auf den nächsten beiden Seiten zunächst den Fall, dass
wir
mit einer ungeraden Zahl potenzieren müssen. Kurz gesagt gilt folgendes:
| Das Potenzieren mit einem
ungeraden Exponenten ist eine Äquivalenzumformung. |
|
 |
Beweis |
|
Im Kapitel 3 des Kurses
Ungleichungen (neues Fenster) haben wir erklärt, dass das
Anwenden einer streng monton steigenden Funktion eine
Äquivalenzumformung ist.
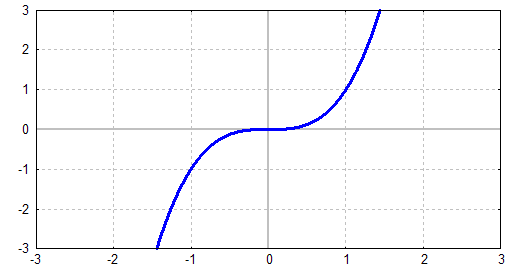
Weil aber ungerade Potenzfunktion streng monoton steigend sind,
ist das Anwennden
einer ungeraden Potenzfunktion eine Äquivalenzumformung. Mit anderen
Worten:
Wir dürfen beide Seiten einer Wurzelungleichung mit einer ungeraden Zahl
potenzieren:
Die Anwendung auf eine "Wurzelungleichung mit ungeradem Exponenten"
zeigen
wir auf der nächsten Seite.
|
|