Potenzieren mit
geraden Exponenten
ist nur dann eine
Äquivalenzumformung,
wenn beide Seiten
der Ungleichung
nicht-negativ sind. |
 |
Satz |
|
Potenziert
man eine Wurzelungleichung mit einer geraden Zahl, dann ist dies nur dann
eine Äquivalenzumformung,
wenn beide Seiten der Ungleichung nicht-negativ sind. |
|
 |
Potenzieren mit geradem
Exponenten |
|
Wir bereits oben erwähnt haben wir im Kurs
Ungleichungen erklärt, dass das Anwenden
einer streng monton steigenden Funktion eine Äquivalenzumformung
ist.
Eine gerade Potenzfunktion ist aber nicht streng-monoton steigend, und
deshalb
darf man ein Ungleichung eigentlich nicht mit einer geraden Zahl
potenzieren:

Man kann aber zumindestens den nicht-negativen Teil einer geraden
Potenzfunktion
anwenden, denn dieser Teil ist streng monton steigend:

Konkret bedeutet dies, dass man eine Ungleichung mit einer geraden Zahl
potenzieren
darf, wenn beide Seiten der Ungleichung nur nicht-negative Werte
annehmen können
(d.h. nur positive Werte oder Null). Beispiel:
Gegeben sei die folgende Wurzelungleichung. Wie wir
sehen, besteht die
Wurzelungleichung aus zwei Wurzeln, wobei je eine
Wurzel auf einer Seite steht.
Konstanten kommen in dieser Wurzelungleichung nicht
vor, sondern nur Wurzeln:
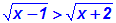
Weil auf beiden Seiten Wurzeln stehen, und Wurzeln laut
ihrer Definition
stets einen nicht-negativen Wert haben, dürfen wir die
Ungleichung mit
der geraden Zahl 2 potenzieren:
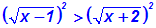
Der Rest des Lösungsweges ist leicht,
wir zeigen ihn auf der nächsten Seite.
Natürlich bestehen nicht alle Wurzelungleichungen aus zwei Wurzeln, d.h.
es ist nicht
immer offensichtlich, ob beide Seiten der Wurzelungleichung positiv
sind. Beispiel:
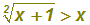
Hier kann man nicht sagen, ob die rechte Seite nicht-negativ ist, denn
sie ist ja variabel.
Deshalb werden wir auf den restlichen Seiten des Kapitels uns einige
Tricks überlegen,
wie man solche Wurzelungleichungen trotzdem lösen kann.
|
|