|
Beide Seiten negativ |
 |
Beispiel |
|
Bis jetzt haben wir immer gesagt, dass beide Seiten einer Ungleichung
nicht-negativ sein müssen, damit ich sie mit einer geraden
Zahl potenzieren darf.
Doch was ist eigentlich mit dem Fall, dass beide Seiten
nicht-positiv
sind,
d.h. wenn beide Seiten negativ oder Null werden können. Beispiel:
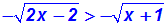
Wir zeigen zwei Lösungen für dieses Problem.
|
 |
Einfache Lösung: mit –1
multiplizieren |
|
Gegeben war die Wurzelungleichung:
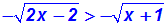
Die einfachste Lösung ist, dass wir beide Seiten mit –1 multiplizieren,
wobei wir nicht vergessen dürfen, das Ungleichheitszeichen umzudrehen
(weil wir ja mit einer negativen Zahl multiplizieren):
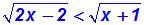
Nun sind beide Seiten nicht-negativ, und wir dürfen mit 2
potenzieren (quadrieren).
|
 |
Komplizierte Lösung (nur
theoretisch interessant) |
|
Gegeben war die Ungleichung:
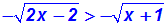
Es gibt noch eine zweite Möglichkeit, diese Ungleichung zu lösen. Aus
dem Kurs
Ungleichungen (Kurs öffnet im neuen Browserfenster) wisssen wir ja
bereits:
Man darf auf
eine Ungleichung eine streng-monoton fallende
Funktion anwenden, wenn man das Ungleichheitszeichen umdreht.
Nun fragen wir uns, ob wir diesen Satz auf die gegebene Ungleichung
anwenden können.
Wenn wir die Ungleichung quadrieren, dann wenden wir eigentlich eine Funktion an
(die Quadratfunktion), die weder streng-monton steigend noch
streng-monoton fallend ist.
Weil aber beide Seiten der gegebenen Ungleichung nicht-positiv (negativ
oder Null) sind,
wenden
wir beim Quadrieren nur
den streng-monoton fallenden Teil dieser
Quadratfunktion an
Das Bild zeigt nochmal, welchen Teil der Quadratfunktion wir anwenden:
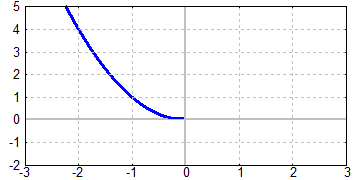
Und weil wir nur eine streng-monoton fallende Funktion anwenden, dürfen wir die
Ungleichung quadrieren, müssen aber - wie gesagt -
das
Ungleichheitszeichen umdrehen:
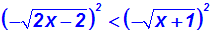
Die negativen Vorzeichen fallen durch das Quadrieren weg.
Wir erhalten die gleiche
Ungleichung wie oben, als wir beide Seiten mit
–1
multipliziert hatten:
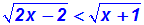
|
|